4-1. 트리란?
트리 구조는 계층적인 관계를 가진 자료의 표현에 매우 유용하게 사용.
트리관련 용어
- 노드 : 트리에서 각각의 요소
- 간선 또는 엣지 : 노드와 노드의 연결 관계
- 루트 노드 : 계층 적인 구조에서 가장 높은 곳에 있는 노드
| 부모 노드 | 간선으로 직접 연결된 노드 중에 상위 노드 |
| 자식 노드 | 간선으로 직접 연결된 노드 중에 하위 노드 |
| 형제 노드 | 같은 부모 노드를 가진 노드 |
| 조상 노드 | 어떤 노드에서 루트 노드까지의 경로상에 있는 모든 노드 |
| 자손 노드 | 어떤 노드 하위에 연결된 모든 노드 |
| 단말 노드 | 자식 노드가 없는 노드. 자식이 있으면 비단말 노드 |
| 노드의 차수 | 노드가 가지고 있는 자식의 수. 단말 노드는 항상 0 |
| 트리의 차수 | 트리에 포함된 모든 노드의 차수 중에서 가장 큰 수 |
| 레벨 | 트리의 각층에 번호를 매기는 것. 루트 노드의 레벨은 항상 1이고 한 층씩 내려갈수록 레벨은 1씩 증가 |
| 트리의 높이 | 트리가 가지고 있는 최대 레벨 |
트리의 표현 방법
- 중첩된 집합으로 표현

- 중첩된 괄호로 표현한 트리
=> (A (B (E) (F) (G(K))) (C(H)) (D(I) (J)))
- 들여쓰기로 나타내기
일반트리의 표현
일반 트리 :자식의 개수에 제한이 없는 트리
- N-링크 표현 : 차수가 N인 노드가 N개의 링크를 갖도록 허용
왼쪽 자식 - 오른쪽 형제 표현
- 하나의 링크는 왼쪽 자식을 가리키고, 다른 하나는 오른족 형제를 가리키기 위해 사용.

04-2 이진트리
이진트리는 모든 노드가 최대 2개의 자식만을 가질 수 있는 트리. 왼쪽 자식과 오른쪽 자식은 반드시 구별 되어야 한다.
알고리즘 : 이진탐색 트리, 힙트리, 수식트리
이진트리 종류
이진트리는 레벨과 노드 수의 관계에 따라 포화 이진 트리와 완전 이진트리를 정의할 수 있다.
- 포화 이진 트리 : 트리의 각 레벨에 노드가 꽉 차 있는 이진 트리.
- 전체 노드 개수 :

- 완전 이진 트리 : 높이가 k인 트리에서 레벨 1부터 k-1까지는 노드가 모두 채워져 있고 마지막 레벨 k에서는 왼쪽부터 오른쪽 으로 노트가 순서대로 채워져 있는 이진 트리이다. 마지막 레벨에서는 노드가 꽉 차 있지 않아도 되지만 중간에 빈 곳이 있으면 안 된다.
- 균형 이진 트리: 균형 이진 트리 또는 높이균형 이진 트리는 모든 노드에서 좌우 서브 트리의 높이 차이가 1 이하인 트리.
이진 트리의 표현 방법
이진 트리배열 구조 표현
- 트리의 높이를 구해 배열(또는 파이썬의 리스트)을 할당한다. 예를 들어, 높이가 k이면 길이가 (2^k)-1인 배열이 필요.
- 포화 이진 트리의 번호를 인덱스로 사용하여 배열에 노드들을 저장.

- 노드 i의 부모 노드 인데스 = i/2
- 노드 i의 왼쪽 자식 노드 인덱스 = 2i
- 노드 i의 오른쪽 자식 노드 인덱스 = 2i +1
- 연결된 구조 표현 : 링크 표현법
- 이진 트리를 위한 노드는 두 개의 링크가 필요한데, 이들은 각각 왼쪽과 오른쪽 자식 노드를 가리킨다.

이진 트리를 위한 노드 클래스
class BTNode:
def __init__(self, elem, left=None, right=None):
self.data = elem
self.left = left
self.right = right4-3. 이진 트리의 연산
이진 트리의 표준순회
-순회 : 모든 노드를 한 번씩 방문
- 전위순회:VLR
- 중위순회:LVR
- 후위순회:LRV
- 전위순회: 루트를 먼저 방문(V)하고 다음에 왼쪽 서브 트리를 방문(L)하고, 방문이 끝나면 마지막으로 오른쪽 서브 트리를 방문(R)하는 방식

def preorder(n):
if n is not None:
print(n.data, end=' ')
preorder(n.left)
preorder(n.right)- 전위순회 결과 : A B D E C F
- 중위순회 : 왼쪽 서브 트리부터 시작해서 루트를 거쳐 오른쪽 서브 트리 순으로 방문.

def inorder(n):
if n is not None:
inorder(n.left)
print(n.data, end=' ')
inorder(n.right)- 후위 순회 : 왼쪽 서브 트리 -> 오른쪽 서브 트리 -> 루트 순으로 방문.
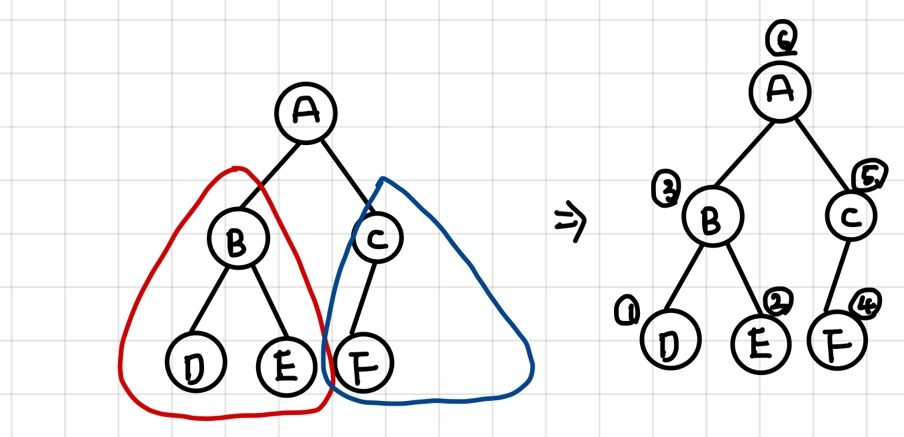
def postorder(n):
if n is not None :
postorder(n.left)
postorder(n.right)
print(n.data, end = ' ')레벨순회
- 레벨 순으로 노드를 방문. 위 그림 예시로 A -> B -> C -> D -> E -> F 순으로 방문
- 큐를 사용 : 최초에 루트인 A가 큐에 입력된 상태에서 순회가 시작. 큐에서 하나를 꺼내면 A가 나오고, A의 자식인 B와 C를 순서대로 큐에 삽입. 다음으로 큐에서 B를 꺼내고, 자식인 D와 E를 넣는다. 이과정은 큐가 공백이 될 때까지 반복.
def levelorder(root):
queue = ArrayQueue()
queue.enqueue(root)
while not queue.isEmpty() :
n = queue.dequeue()
if n is not None:
print(n.data, end=' ')
queue.enqueue(n.left)
queue.enqueue(n.right)이진 트리의 연산들
- 이진 트리의 노드 개수는 왼쪽 서브 트리의 노드 수와 오른쪽 서브 트리의 노드 수의 합에 1(루트노드)을 더하면 된다.
def count_node(n):
if n is None:
return 0
else:
return count_node(n.left) + count_node(n.right) + 1- 이진 트리의 높이는 왼쪽 서브 트리의 높이와 오른쪽 서브 트리의 높이 중에서 큰 값에 1을 더한 값.
def calc_height(n):
if n is None:
return 0
hLeft = calc_height(n.left)
hRight = clac_height(n.right)
if (hLeft > hRight):
return hLeft + 1
else: return hRight + 1
'CS공부🖥️ > 자료구조' 카테고리의 다른 글
| 자료구조와 알고리즘 with 파이썬 chapter6. 정렬 (0) | 2025.02.02 |
|---|---|
| 자료구조와 알고리즘 with 파이썬 chapter5. 알고리즘 개요 (1) | 2025.01.24 |
| 자료구조와 알고리즘 with 파이썬 chapter3 (0) | 2025.01.09 |
| 자료구조와 알고리즘 with 파이썬 chapter2 (1) | 2025.01.03 |
| 자료구조와 알고리즘with 파이썬 chapter1 (0) | 2025.01.02 |


